activation function

설명 필요, linearity, non linearity

sigmoid function

대충 설명

katex

\[ h(x) = \frac {1} {1+e^{-x}} \]

chain rule을 통해서 기본식에서 derivative 식까지 이해해보기

\[\begin{split} \begin{equation} \begin{split} h'(x) &= \frac {\partial} {\partial x} h(x) \\ &= \frac {\partial} {\partial x} \Big[ \frac {1} {1+e^{-x}} \Big]=\frac {\partial} {\partial x} (1+e^{-x})^{-1}\\ &= -1 *(1+e^{-x})^{-2}(-e^{-x})\\ &= \frac {-e^{-x}} {-(1+e^{-x})^2} = \frac {e^{-x}} {(1+e^{-x})^2}\\ &= \frac {1} {1+e^{-x}} \frac {e^{-x}} {1+e^{-x}}\\ &= \frac {1} {1+e^{-x}} \frac {1+e^{-x}-1} {1+e^{-x}}\\ &= \frac {1} {1+e^{-x}} \Big[ \frac {(1+e^{-x})} {1+e^{-x}} - \frac {1} {1+e^{-x}} \Big]\\ &= \frac {1} {1+e^{-x}} \Big[ 1 - \frac {1} {1+e^{-x}} \Big]\\ &=h(x)(1 - h(x)) \\ \end{split} \end{equation} \end{split}\]

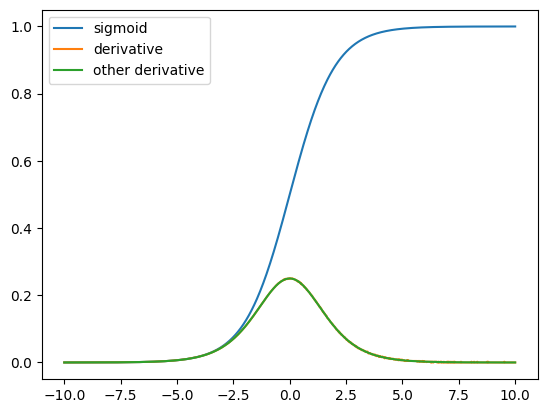
numpy로 그래프 그려보기

import numpy
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1+numpy.exp(-x))

def sigmoid_derivative(x,step):
    return (sigmoid(x + step) - sigmoid(x)) / step

def other_derivative(x):
    y = [(1 / (1 + numpy.exp(-i))) * (1 - (1 /(1 + numpy.exp(-i)))) for i in x]
    return y

x = numpy.linspace(-10, 10, 1000)

y1 = sigmoid(x)
y2 = sigmoid_derivative(x, 0.0000000000001)
y3 = other_derivative(x)

plt.plot(x, y1, label='sigmoid')
plt.plot(x, y2, label='derivative')
plt.plot(x, y3, label='other derivative')
plt.legend(loc='upper left')
plt.show()