최소비용경로 문제

최소비용경로 문제#

Queue 큐#

기본적으로 Queue라는 것은 선입선출(FIFO)의 구조를 가지는 자료형을 말한다. 어떤 조건이 없을때는 먼저 들어온 순서대로 마치 줄을 서는 것 처럼 대기열(queue)에 들어가고, 들어간 순서대로 나오는 것을 말한다. 큐를 사용하면 위와 같은 특징으로 인해서 비동기 메세징, 스트리밍, 너비우선탐색(BFS:breath first search) 등의 소프트웨어 개발에서 널리 사용되고 있다. 파이썬 doc에서는 정보가 여러 스레드 간에 안전하게 교환되어야 할 때 스레드 프로그래밍에 특히 유용하다고 말한다.

파이썬에서 제공하는 queue모듈은 thread-safe하게 설계되어있다. 이는 여러 스레드에서 동시에 접근해도 안전하게 데이터를 처리하도록 설계되어있다는 것을 의미한다. 그러나 이러한 thread-safe한 특성 때문에 오버헤드가 있을 수 있다. 단일 스레드에서만 작동하는 경우, 순수한 성능 최적화를 원한다면 다른 방법을 사용하는 것이 추천된다.

파이썬에서는 3개의 queue를 기본적으로 class로 구현해놓고 있다.

  1. class queue.Queue(maxsize=0)

    • the first tasks added are the first retrieved.(FIFO)

  2. class queue.LifoQueue(maxsize=0)

    • the most recently added entry is the first retrieved (operating like a stack)

  3. class queue.PriorityQueue(maxsize=0)

    • the entries are kept sorted (using the heapq module) and the lowest valued entry is retrieved first.

  4. class queue.SimpleQueue : 이거는 단순큐로 작업 추적과 같은 고급기능은 뺀 것이다.

  5. exception queue.Empty : get()이 비어있는 queue 객체에 call 될때 발생하는 예외

  6. exception queue.Full : put()이 가득 찬 queue 객체에 호출될 떄 발생하는 예외

method

설명

Queue.qsize()

큐의 대략의 크기

Queue.empty()

비어 있으면 True를, 그렇지 않으면 False를 반환

Queue.full()

가득 차면 True를, 그렇지 않으면 False를 반환

Queue.put(item, block=True, timeout=None)

항목을 넣어줌 - Enqueue

Queue.get(block=True, timeout=None)

항목을 제거하고 반환 - Dequeue

Queue.join()

모든 항목을 꺼내서 처리할 때까지 블록

deque#

from collections import deque

위에서 Queue 내장 모듈에 대해서 알아봤는데, 기본적으로 thread-safe한 특징을 가지며, 내부적으로는 리스트를 사용하여 구현되어있다. 빈번하게 put, get으로 enqueue, dequeue 연산을 수행하게 되면 리스트의 자료구조적 한계로 O(1)보다 시간이 더 걸릴 수 있다. 이를 위해서 collections.deque를 사용하여 큐를 구현하여 사용하는 것이 좋다. 얘는 양끝에서 enqueue dequeue하는데 O(1)의 시간 복잡도를 보장한다.

collections.deque는 굉장히 빠른 장점을 가진 리스트형+내장형 파이썬 객체이다. deque는 스택과 큐를 일반화 한 것으로 double-ended queue를 말한다. 이름 그대로 queue이긴 한데 앞 뒤가 뚫려있고, 앞 뒤로 삭제 및 삽입 그리고 신기하게도 회전도 할 수 있어서 원형 큐와 같은 문제를 만났을 때 편하게 해준다. queue 위의 세 개는 모른다고 쳐도 deque를 어떻게 사용하는지는 알고 있는 것이 좋다.

deque는 앞에서 말했듯이 O(1)의 성능을 가진다. 리스트가 O(n)의 성능인 것을 생각해보면 속도면으로 굉장한 차이가 있고, method도 크게 리스트와 차이가 없다는 것을 보면 알 수 있다. 대부분의 stack이나 queue를 사용해야할 경우에는 deque를 사용해서 시도해보는 것을 기본 스탠스로 가져가자.

method

설명

비고

append(x)

데크의 오른쪽에 x를 추가

appendleft(x)

데크의 왼쪽에 x를 추가

리스트엔없음

clear()

데크에서 모든 요소를 제거하고 길이가 0인 상태

copy()

데크의 얕은 복사본

count(x)

x 와 같은 데크 요소의 수를 셉

extend(iterable)

iterable 인자에서 온 요소를 추가하여 데크의 오른쪽을 확장

extendleft(iterable)

iterable에서 온 요소를 추가하여 데크의 왼쪽을 확장. index변경

리스트엔없음

index(x[, start[, stop]])

데크에 있는 x의 위치를 반환

insert(i, x)

x를 데크의 i 위치에 삽입.길이의 데크가 maxlen 이상으로 커지면, IndexError가 발생

pop()

오른쪽에서 요소를 제거하고 반환

popleft()

왼쪽에서 요소를 제거하고 반환

remove(value)

value의 첫 번째 항목을 제거

리스트엔없음 원형큐로서 사용가능

reverse()

요소들을 제자리에서 순서를 뒤집고 None을 반환

reversed(d)도 가능

rotate(n=1)

n 단계 오른쪽으로 회전합니다. n이 음수이면, 왼쪽으로 회전

maxlen

최대 크기 또는 제한이 없으면 None

deque(maxlen=n)

in

내부 요소 논리적 검사

d[n]

n번째 요소 반환

양끝은 O(1) 이지만 중간은 O(n)으로 리스트와 비슷

Priority Queue 우선순위 큐#

우선순위 큐는 들어간 순서와는 상관없이 우선순위가 높은 데이터가 먼저 나오는 것을 말한다. First in 보다는 First Priority가 중요한 것이다.

우선순위 큐는 heap이라는 자료구조를 가지고 구현할 수 있기 때문에 둘은 밀접한 관계를 가지고 항상 같이 언급되곤 한다. 그렇기 때문에 밑에서는 heap에 대한 설명을 하고 나서 우선순위 큐에 대한 설명을 이어나가겠다.

우선순위큐는 각 요소가 우선순위를 가진 데이터의 집합을 말한다. 이 집합에서 가장 높은 우선순위를 가진 요소를 꺼내올 수 있으며, 이는 문제의 경우가 데이터를 enqueue,dequeue할때 우선순위에 따라 결정되어야할 경우일 때 효율적이다. 배열 연결리스트 힙등으로 다양한 방법으로 구현될 수 있지만 가장 이상적인 방법은 heap을 이용하는 방법이다.

그렇다면 heap은 무엇인가? 힙이란 완전 이진 트리 형태로 특정한 규칙(최대,최소)을 만족하는 배열을 말한다.

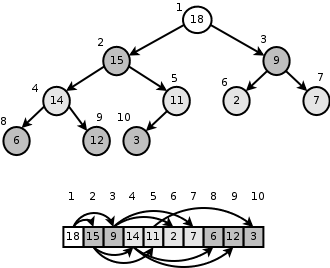
https://users.cecs.anu.edu.au/~Alistair.Rendell/Teaching/apac_comp3600/module2/images/Heaps_HeapStructure.png

Fig. 18 heap에 대한 설명#

\[\begin{split} \text{모든 k에 대해}\\ heap[k] <= heap[2*k+1]\\ heap[k] <= heap[2*k+2]\\ \text{인 배열을 사용} \end{split}\]

최대힙의 경우에는 부모노드의 키 값이 자식 노드의 키 값보다 항상 크거나 같고, 최소힙의 경우에는 부모노드의 키 값이 항상 자식노드의 키보다 작거나 같은 것을 말한다. 그렇기 때문에 수치적으로 우선순위를 부여하는데 최적화 된 자료구조라고 볼 수 있다.

Heapq#

heapq는 표준라이브러리 중 하나로 heap 연산을 위한 함수들을 제공한다. 리스트를 힙처럼(heapify) 다룰 수 있다. 주로 min-heap을 지원하며 이를 통해서 우선순위 큐를 효율적으로 구현할 수 있다.

여기서 제공하는 api는 두 가지 측면에서 교과서 힙 알고리즘과 다르다고 한다.

  1. 0부터 시작하는 인텍싱을 사용한다. 이것은 노드의 인덱싱과 자식의 인덱스 사이의 관계를 불분명하게 만들긴 하지만, 파이썬이 0부터 시작하니깐 오케이다.

  2. pop method는 가장 큰 항목이 아니라 가장 작은 항목을 반환한다. 이는 기본적인 heapq의 반환물이 min-heap이기 때문이다.

method

설명

비고

heapq.heapify(x)

리스트 x를 선형 시간으로 제자리에서 힙으로 변환

heapq.heappush(heap, item)

힙 불변성을 유지하면서, item 값을 heap으로 푸시

heapq.heappop(heap)

불변성을 유지하면서, heap에서 가장 작은 항목을 팝하고 반환합\팝 하지 않고 가장 작은 항목에 액세스하려면, heap[0]을 사용

heapq.heappushpop(heap, item)

힙에 item을 푸시한 다음, heap에서 가장 작은 항목을 팝하고 반환

기본적으로 두개 나눠서 하는 것보다 효율적

heapq.heapreplace(heap, item)

가장 작은 항목을 팝하고 반환하며, 새로운 item도 푸시합니다. 힙 크기는 변경되지 않음

고정크기를 유지할때

heapq.merge(*iterables, key=None, reverse=False)

heapq.nlargest(n, iterable, key=None)

n 개의 가장 큰 요소로 구성된 리스트를 반환

heapq.nsmallest(n, iterable, key=None)

n 개의 가장 작은 요소로 구성된 리스트를 반환

heapsort#

def heapsort(iterable):
    h = []
    for value in iterable:
        heappush(h, value)
    return [heappop(h) for i in range(len(h))]

heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])

>>> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

안정적인 정렬?

안정적인 정렬이란

입력 데이터 내에서 동일한 값들 사이에 원래 순서가 정렬 후에도 보존된다는 것

하나의 키값(나이)로 정렬된 상태의 데이터를 새로운 키값(성)으로 정렬을 수행했을 때, 나이에 대한 정렬이 유지될 수 있어야 안정된 정렬이라고 말할 수 있다.

heapsort는 그렇게 하지 못하고 sorted는 그럴수 있다고 말한다.

sorted는 2002년 Tim Peters에 의해 개발된 merge sort + insertion sort 식의 하이브리드 정렬 알고리즘으로 1) 이미 부분정렬에 대해서는 더 빠르게 동작하고 2) 같은 키값의 정렬에 대해서는 순서를 보존하는 3) \(O(n logn)\)(최악일 경우에도)의 시간복잡도를 가지는 정렬이다.

  1. 리스트를 작은 부분으로 나누고

  2. 각 부분 리스트를 삽입 정렬한다.

  3. 이후 병합 정렬로 하나의 리스트로 만든다.

이러한 특성으로 안정적이면서도 부분적으로 정렬된 경우에는 효율적인 정렬로서 기본 정렬로 파이썬이 사용하는 거이다.

dijkstra 다익스트라#

그래프의 한 지점에서 갈 수 있는 모든 지점에 대해서 최단 거리를 구하는 알고리즘

  1. 시작점은 0, 나머지는 INF

  2. 시작점과 연결된 정점들과의 간선 비용 업데이트

  3. 가장 거리가 짧은 정점을 선택하여 연결되어 있는 모든 정점들의 거리를 계산

  4. 거리가 더 짧아질 경우 업데이트, 아니면 넘어간다

  5. 3번으로 돌아가 모든 정점들의 거리를 업데이트

  6. 모든 정점을 확인하면 종료

다익스트라 알고리즘에는 우선순위큐가 사용된다. 가장 짧은 거리를 가진 정점을 업데이트 해야하기 때문에 최소값을 가진 것이 위로 도출되는 것이 편하기 때문에 해당 자료구조를 사용하는 것이다. 우선순위큐를 사용하기 위해 heappop, heappush를 사용한다.

referances#

Contents