Resnet

Resnet#

Deep Residual Learning from Image Recognition

Abstract

Deeper neural networks are more difficult to train. We present a residual learning framework to ease the training of networks that are substantially deeper than those used previously(vgg). We explicitly reformulate the layers as learning residual functions with reference to the layer inputs, instead of learning unreferenced functions. We provide comprehensive empirical evidence showing that these residual networks are easier to optimize, and can gain accuracy from considerably increased depth. On the ImageNet dataset we evaluate residual nets with a depth of up to 152 layers - 8×deeper than VGG nets [41] but still having lower complexity. An ensemble of these residual nets achieves 3.57% error on the ImageNet testset. This result won the 1st place on theILSVRC 2015 classification task. We also present analysis on CIFAR-10 with 100 and 1000 layers.The depth of representations is of central importance for many visual recognition tasks. Solely due to our extremely deep representations, we obtain a 28% relative improvement on the COCO object detection dataset. Deep residual nets are foundations of our submissions to ILSVRC& COCO 2015 competitions 1, where we also won the 1st places on the tasks of ImageNet detection, ImageNet localization, COCO detection, and COCO segmentation.

Deep Residual Learning for Image Recognition 이란 제목의 논문으로 우리가 많이 들어본 ‘resnet’에 대해 나온 논문이다. 2014년에 vgg논문이 나오고 바로 다음 해에 나온 논문으로, 사실상 vgg의 구조에 residual mapping이라는 아이디어만을 추가하고도 imagenet classification에서 눈에 띄는 점수 향상을 보였다. resnet이라는 논문은 아이디어 자체가 쉽다는 점, 그리고 그 아이디어가 당시의 모델의 깊이와 모델의 성능이 선형적인 상관관계를 이루지 못하는 문제(degradation problem)를 쉬운 논리로 해결한다는 점에서 좋은 논문으로 지금까지 평가된다. 우선은 resent에서 해결하고자 하는 문제부터 살펴보자.

문제 설정 problem set-up#

vgg를 통해서 image classification이라는 과제에서 많은 breakthrough가 있었다. cnn layer를 깊이 쌓음으로써 low/mid/high 수준의 feature들을 통합하고, 더 깊이 쌓을수록 더 많은 feature들을 data에서 추출할 수 있게 된 것이다. 하지만 무조건 깊이를 많이 쌓는다고 되었던 것은 아니다. 밑의 2개의 문제가 그것이다.

1. vanishing/exploding gradients problem#

Is learning better networks as easy as stacking more layers?

—bro. of course not!

첫번째 문제는 gradient가 소실되거나 폭발해버리는 문제다. layer가 몇 층 되지 않는 shallow한 network에서는 이러한 문제가 나타나지 않거나 걱정이 필요없을 정도 이지만, network가 깊어지면 gradient(경사도)가 too small or big for training to work effectively하게 되고 이 문제가 vanishing exploding gradient 문제다. sigmoid 함수를 생각하면 문제에 대해 이애하기 쉽다.

when n hidden layers use an activation like the sigmoid function, n small derivatives are multiplied together. Thus, the gradient decreases exponentially as we propagate down to the initial layers.

chain rule에 따라 각 layer상에서의 derivative는 네트워크를 따라서 곱해지고, 방향성은 끝단에서 맨 처음 layer로 향하게 된다. 뒤에서부터 앞으로 향하는 back propagation에서 sigmoid를 non-linear activaiton function으로 사용하면, 음의 x값(input)들은 전부 0에 한없이 가까워지기 때문에 활성화가 잘되지 않고, 곱셈이 진행됨에 따라 아주아주 작아지게된다. 이는 곧 맨 앞까지 오면 gradient가 사라진 것 처럼, 그리고 활성화 역할을 제대로 하지 못하는 효과를 나타낸다.

하지만 이러한 문제는 논문상에서는 많이 해결되었다고 말한다. 학습 자체가 안되는 문제이고 gradient를 살리는 것이 문제임으로 nomarlized initialization, intermediate normalization layers 이 두 방법에서 해결되었다고 본다. 논문에서 주로 다루고자하고 해결하고 싶은 문제는 2번쨰 문제이다.

2. Degradation problem#

깊은 network이 수렴을 시작한다고해도, degradation problem(성능 저하 문제)가 나타날 수 있다고 말한다. 이 문제는 gradient vanishing/exploding 문제보다 좀 더 넓은 범위의 문제이다. 이 문제의 상황에서 network는 학습도 되고, gradient도 살아있고, accuracy score가 상승은 하는데, 오히려 depth가 낮은 network보다 depth를 높인 network가 정확도 등의 평가지표에서 더 높아야 하는데 그렇지 못하는 현상을 말한다.

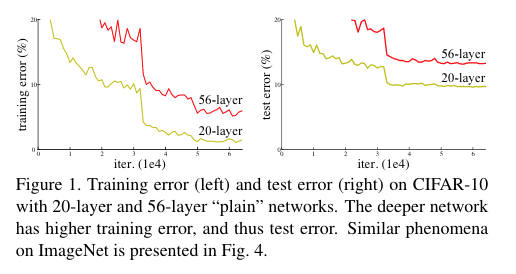
../../_images/resnet_1.png — Fig. 7 56 layer network가 20 layer network보다 error율이 높은 것을 확인할 수 있다. 성능이 더 잘 안나온 것이다.#

deeper is better를 하나의 요소만 넣으면 가능하게 하는 것, 즉 degradation problem을 해결하는 것 - 이 논문에서는 Redisual mapping이다.

Residual mapping, Identity mapping#

input과 output을 포함하는 함수라고 생각하면 된다.

한 영역의 요소를 다른 영역의 요소와 연결하는 과정 혹은 함수이다. y = f(x) 라는 식을 본다면 x input을 y로 바꾸는 함수 자체가 mapping이라고 할 수 있고, x(input)는 f(function)라는 mapping, 함수를 통과함으로써 y(output)가 된다.

image classification 에서는 input(이미지) \(\to\) label(number) 자체가 하나의 mapping이라고 볼 수 있다. 이런 대응관계를 mapping이라고 보면 된다. 일반적인 수학에서는 하나의 함수가 mapping function으로 볼 수 있고, 딥러닝에서는 크게보면 모델이 mapping function이라고 볼 수 있다. 다만 좀 복잡한 non-linear mapping function이라고 볼 수 있겠다. 딥러닝에서는 아키텍쳐, 가중치, 활성화 함수 등에 의해 결정된다. 또한 적절한 output을 위해 최적화 과정이 필요하다.

그렇다면 identity mapping(항등 매핑)은 무엇일까? 항등매핑 그러니깐 수학적으로 표현하면 \(y=f(\text{x})=\text{x}\)이라고 볼 수 있다.

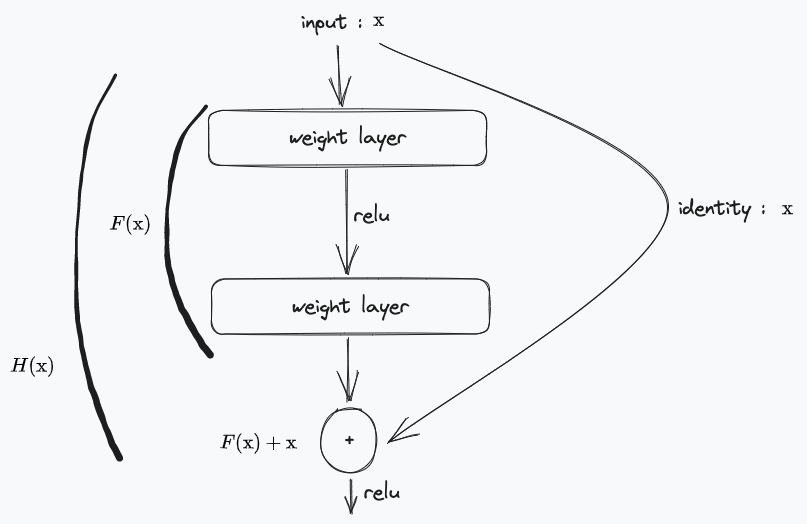
../../_images/resnet_2.png — Fig. 8 obsidian으로 내맘대로 그려본 fig2#

기존의 vgg에서의 mapping block을 \(H(\text{x})\)이라고 한다면, 이런 block이 18개정도 이어져 붙어있는 형태였다. block 내부에는 cnn layer + relu layer + cnn layer + relu layer 로 구성되어 있다.

resent에서는 이러한 구조에서 block마다의 input(x) \(\to\) output(\(H(\text{x})\)=y) 관계를 분해한다. input(x) + residual(F(x)) \(\to\) output(\(H(\text{x})\)=y). 결국 하나의 블럭 상에서 학습해야하는 부분은 \(H(\text{x}) - x = F(\text{x})\)가 되는 것이고 이것이 Residual이 되는 것이다. 그리고 input은 y=f(x)=x 처럼 input값이 output과 같은 것 처럼 mapping되는 부분임으로 identity mapping이라고 불린다.

\[\begin{split} \begin{gather} \tag{residual mapping in fig2}F = W_2\sigma(W_1 x)\\ \tag{a building block} \text{y} = W_2\sigma(W_1\text{x}) + x\\ \tag{Equ 1}\text{y} = F(\text{x},\{ W_i \}) + \text{x} \\ \tag{Equ 2} \text{y} = F(\text{x},\{ W_i \}) + W_s\text{x} \end{gather} \end{split}\]

F : residual function
만약 F가 single layer라면 : y = W_1 x + x 가 될 수도 있다.
F(x, {W_i})는 multiple convolutional layers를 표현

기존의 output에다 input을 더해주는 +의 개념으로 이해할 수 도 있고, 기존의 mapping을 해체하는 -의 개념으로 생각해볼 수 도 있다. -의 개념으로 접근한다면 기존에 optimize 해 주어야할 부분이 줄어든다는 관점으로 접근할 수 있을 것이고, 이것이 논문에서 가정하고 접근한 지점이다. identity mapping(x)가 이미 optimal하게 mapping을 진행해왔다면 남은 residual mapping(F(x))만 0에 가깝게 만들면 된다는 것이다. 그럼 H(x)가 결과적으로 optimal해질 것이고 output은 x로 되어서 다음 block의 input이 될 것이다.

The degradation problem suggests that the solvers might have difficulties in approximating identity mappingsby multiple nonlinear layers.

여기서 solver란 optimization algorithm, back-propagation algorithm을 말한다. gradient를 계산하여 가중치를 업데이트하여 손실 함수를 최소화하는 과정을 말한다. 즉 기존의 identity mapping이 없던 network에서의 최적화 과정에서의 degradation problem은 비선형 레이어를 여러 개 통과하면서 입력과 출력이 같은(identity mapping)의 경우에 대한 대처가 어려워 진다는 것이다. 그리고 위의 residual mapping과 identity mapping을 shortcut connection으로 구현함으로써 깊어지는 network에서의 gradient 흐름을 보존할 수 있었다고 말한다.

물론 identity mapping이 optimal할 경우는 실제 학습과정에서는 이루어 지지 않을 수 있다고 말다. 하지만 그럼에도 불구하고 기존의 input값을 참조하는 것 만으로도 학습에 도움이 된다고 논문에서는 말한다. 다음 블록의 residual mapping이 이전 블록의 identity mapping을 참조하는 것 만으로도 학습의 요동(?)이 적어진다고 말한다.

shortcut connection == identity mapping?#

shortcut connection은 입력값을 뒤로 넘겨서 더해준다. 이것에도 종류가 있고 identity mapping은 1번으로 그 종류중에 하나로 볼 수 있음으로 정확히는 차이가 존재한다. input과 output의 dimension이 달라지면 고려해야할 것이 많아진다.

Identity Shortcut Connection (핵심): Identity Shortcut Connection은 이전 레이어의 출력을 현재 레이어의 입력에 직접 더해주는 방식입.
Projection Shortcut Connection: Projection Shortcut Connection은 이전 레이어의 출력을 현재 레이어의 입력에 선형 변환(projection)하여 크기나 차원을 맞춘 후 더해주는 방식. 이는 차원이 다른 경우에 사용되며, 선형 변환을 통해 차원 일치를 유지하고 그래디언트 흐름을 보존할 수 있다.
Dimension Matching Shortcut Connection: Dimension Matching Shortcut Connection은 이전 레이어의 출력과 현재 레이어의 입력의 차원이 다를 경우, 차원을 맞추기 위해 추가적인 연산을 수행하는 방식. 이는 차원이 다른 경우에 사용되며, 차원을 일치시켜 그래디언트 흐름을 보존하고 정보의 손실을 최소화.
Skip Connection: Skip Connection은 이전 레이어의 출력을 현재 레이어의 입력으로 바로 전달하는 방식. Identity Shortcut Connection은 Skip Connection의 한 종류로 볼 수 있다. Skip Connection은 네트워크의 여러 레이어를 건너뛰어 그래디언트 흐름을 더 짧게 만들어 줌으로써 그래디언트 소실 문제를 완화시키고, 정보의 손실을 줄일 수 있다.

이전의 연구들에서 shortcut connection은 ‘highway networks’에서 gating function으로 이용되었다고 한다. 이 gates들은 data-dependent하고 parameter가 있었으며 닫힐 수 있었다고 한다. 하지만 resnet에서의 shortcut connection은 parameter-free, never closed라고 한다.

code#

# https://github.com/pytorch/vision/blob/main/torchvision/models/resnet.py
from functools import partial
from typing import Any, Callable, List, Optional, Type, Union

import numpy
import pandas
import torch
import torch.nn as nn
from torch import Tensor

def conv3x3(in_planes: int,
            out_planes: int,
            stride: int = 1,
            groups:int = 1,
            dilation: int = 1) -> nn.Conv2d:
    """3x3 convolution with padding"""
    return nn.Conv2d(in_planes, out_planes,
                     kernel_size=3,
                     stride=stride,
                     padding=dilation,
                     groups=groups,
                     bias=False,
                     dilation=dilation,
                     )

def conv1x1(in_planes: int,
            out_planes: int,
            stride: int = 1,) -> nn.Conv2d:
    """1x1 convolution"""
    return nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=stride, bias=False)

class BasicBlock(nn.Module):
        expansion: int = 1
        
        def __init__(
                self,
                inplanes: int,
                planes: int,
                stride: int = 1,
                downsample: Optional[nn.Module] = None,
                groups: int = 1,
                base_width: int = 64,
                dilation: int = 1,
                norm_layer: Optional[Callable[...,nn.Module]] = None,
        ) -> None:
                super().__init__()
                if norm_layer is None:
                        norm_layer = nn.BatchNorm2d
                if groups != 1 or base_width != 64:
                        raise ValueError("BasicBlock only supports groups=1 and base_width=64")
                if dilation > 1:
                        raise NotImplementedError("Dilation > 1 not supported in BasicBlock")
                # Both self.conv1 and self.downsample layers downsample the input when stride != 1
                self.conv1 = conv3x3(inplanes, planes, stride)
                self.bn1 = norm_layer(planes)
                self.relu = nn.ReLU(inplace=True)
                self.conv2 = conv3x3(planes, planes)
                self.bn2 = norm_layer(planes)
                self.downsample = downsample
                self.stride = stride
                
        def forward(self, x: Tensor) -> Tensor:
                identity = x
                
                out = self.conv1(x)
                out = self.bn1(out)
                out = self.relu(out)
                
                out = self.conv2(out)
                out = self.bn2(out)
                # residual function
                
                if self.downsample is not None:
                        identity = self.downsample(x)
                        
                out += identity # identity mapping
                out = self.relu(out)
                return out
                

Implementation#

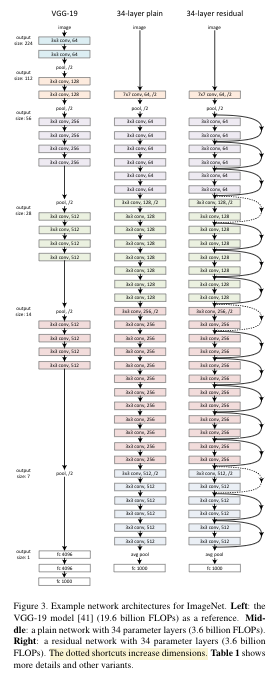
../../_images/resnet_3.png — Fig. 9 vgg19(19.6B FLOPs) - plain 34 layers(3.6B FLOPs) - with shortcut 34 layers(3.6B FLOPs). dotted line이 dimension이 늘어나는 부분이고 이 부분은 equ2 \(W_s\) 1x1 convolutions로 맞춰주었다고 한다.#

in training

he image is resized with its shorter side ran-domly sampled in for scale augmentation.A 224×224 crop is randomly sampled from an image or its horizontal flip, with the per-pixel mean subtracted.
standard color augmentation
conv \(\to\) Batch Normalization \(\to\) non-linear activation f
- plain 네트워크에서도 사용됨으로써 실험자체가 gradient vanishing problem 보다는 degradation problem에 집중하도록 함.
- ensures forward propagated signals to have non-zero variances.
- 입력 데이터의 분산을 조정하여 gradient의 크기를 안정화하여 gradient vanishing problem을 완화하며, 작은 변화에는 덜 민감한 강겅한 모델을 만들고, 빠르게 수렴하도록 돕는 역할을 한다.
- 또한 backward propagated gradients(역전파된 손실함수 최소화 가중치 미분값)가 건강하고 적절한 크기를 유지하는 데 도움된다.
weitght initialization
SGD with mini-batch 256 size
0.1 lr with 10 error plateaus
60 x 10^4 iter
0.0001 weight decay, momentum 0.9
no dropout

in testing

standard 10-crop testing
fully convolutional form
average scores at multiple scales{224,256,384,480,640}

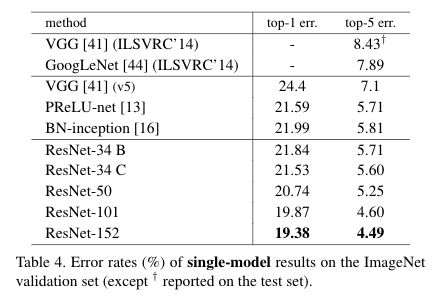
(A) zero-padding shortcuts are usedfor increasing dimensions, and all shortcuts are parameter-free
(B) projec-tion shortcuts are used for increasing dimensions, and othershortcuts are identity
© all shortcuts are projection

위에서 보이는 ABC는 shortcut connection을 어떻게 구성했는지가 다르고, c로 갈수록 성능은 나아졌지만, B만으로도 유의미한 문제 해결을 보임으로 모든 shortcut이 projection shortcut이 될 필요는 없다고 말한다. 해당 논문 이후에 나온 fishnet이라는 논문에서는 C의 방식을 적극채용해서 resnet보다 성능을 높였다.

Deeper Bottleneck Architectures#

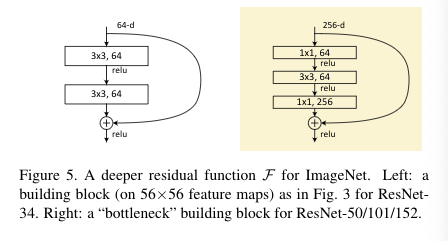
../../_images/resnet_bottleneck.png — Fig. 10 Bottlenect desingn for deeper network architecture#

../../_images/resnet_50.png — Fig. 11 The architecture of ResNet-50-vd. (a) Stem block; (b) Stage1-Block1; © Stage1-Block2; (d) FC-Block.#

18, 34 layers에서는 3x3,3x3로 2개의 conv layer들을 쌓아서 만들었었다면, 더 나아가서 50,101,152 layers를 위해서 1x1,3x3,1x1 를 하나의 블록으로 사용한다. 이것을 bottleneck block 이라고 부른다.

(linear projection conv)1x1 첫번째 filter layer는 input의 차원을 줄이거나 늘리는데(차원을 맞추는데) 사용된다. 이를 통해 계산 비용을 줄이고, 더 적은수의 필터를 사용해서 특징을 추출하는 것이 가능하다.이 과정에서 일부 정보의 손실이 발생할 수는 있다.

두번째 3x3 filter layer는 bottleneck 역할을 실질적으로 하는 공간으로 차원이 줄어든다. 차원이 줄어든다는 것은 feature 특징을 추출하는 것이 적어진다는 것이며, 가중치가 큰 feature에 집중하게 된다. 점차적으로 output size가 112x112 \(\to\) 56x56 \(\to\) 28x28 \(\to\) 14x14 \(\to\) 7x7 로 줄어들면서 cnn의 기본적인 역할(공간적인 특징 학습)에 충실하게 된다.

마지막 1x1 filter layer는 줄어든 차원을 다시 늘려주면서 차원을 보존한다.

resnet50의 구조도를 찾은 것인데 논문에서는 stage구분이 없었는데 이것은 구분을 해서 batch norm등을 다르게 사용하고 있는 것으로 표현되고 있다.

Code#

class Bottleneck(nn.Module):
    expansion: int = 4
    
    def __init__(
        self,
        inplanes: int,
        planes: int,
        stride: int = 1,
        downsample: Optional[nn.Module] = None,
        groups: int = 1,
        base_width: int = 64,
        dilation: int = 1,
        norm_layer: Optional[Callable[..., nn.Module]] = None,
        ) -> None:
        super().__init__()
        if norm_layer is None:
            norm_layer = nn.BatchNorm2d
        width = int(planes * (base_width / 64.0)) * groups
        
        self.conv1 = conv1x1(inplanes, width)
        self.bn1 = norm_layer(width)
        self.conv2 = conv3x3(width, width, stride, groups, dilation)
        self.bn2 = norm_layer(width)
        self.conv3 = conv1x1(width, planes * self.expansion)
        self.bn3 = norm_layer(planes * self.expansion)
        self.relu = nn.ReLU(inplace=True)
        self.downsample = downsample
        self.stride = stride
        
    def forward(self, x: Tensor) -> Tensor:
        identity = x
        
        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)
        
        out = self.conv2(out)
        out = self.bn2(out)
        out = self.relu(out)
        
        out = self.conv3(out)
        out = self.bn3(out)
        
        if self.downsample is not None:
            identity = self.downsample(x)
            
        out += identity
        out = self.relu(out)
        return out

class ResNet(nn.Module):
    def __init__(
        self,
        block: Type[Union[BasicBlock, Bottleneck]],
        layers: List[int],
        num_classes: int = 1000,
        zero_init_residual: bool = False,
        groups: int = 1,
        width_per_group: int = 64,
        replace_stride_with_dilation: Optional[List[bool]] = None,
        norm_layer: Optional[Callable[..., nn.Module]] = None,
    ) -> None:
        super().__init__()
        # _log_api_usage_once(self)
        if norm_layer is None:
            norm_layer = nn.BatchNorm2d
        self._norm_layer = norm_layer

        self.inplanes = 64
        self.dilation = 1
        if replace_stride_with_dilation is None:
            # each element in the tuple indicates if we should replace
            # the 2x2 stride with a dilated convolution instead
            replace_stride_with_dilation = [False, False, False]
        if len(replace_stride_with_dilation) != 3:
            raise ValueError(
                "replace_stride_with_dilation should be None "
                f"or a 3-element tuple, got {replace_stride_with_dilation}"
            )
        self.groups = groups
        self.base_width = width_per_group
        self.conv1 = nn.Conv2d(3, self.inplanes, kernel_size=7, stride=2, padding=3, bias=False)
        self.bn1 = norm_layer(self.inplanes)
        self.relu = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        self.layer1 = self._make_layer(block, 64, layers[0])
        self.layer2 = self._make_layer(block, 128, layers[1], stride=2, dilate=replace_stride_with_dilation[0])
        self.layer3 = self._make_layer(block, 256, layers[2], stride=2, dilate=replace_stride_with_dilation[1])
        self.layer4 = self._make_layer(block, 512, layers[3], stride=2, dilate=replace_stride_with_dilation[2])
        self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
        self.fc = nn.Linear(512 * block.expansion, num_classes)

        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode="fan_out", nonlinearity="relu")
            elif isinstance(m, (nn.BatchNorm2d, nn.GroupNorm)):
                nn.init.constant_(m.weight, 1)
                nn.init.constant_(m.bias, 0)

        # Zero-initialize the last BN in each residual branch,
        # so that the residual branch starts with zeros, and each residual block behaves like an identity.
        # This improves the model by 0.2~0.3% according to https://arxiv.org/abs/1706.02677
        if zero_init_residual:
            for m in self.modules():
                if isinstance(m, Bottleneck) and m.bn3.weight is not None:
                    nn.init.constant_(m.bn3.weight, 0)  # type: ignore[arg-type]
                elif isinstance(m, BasicBlock) and m.bn2.weight is not None:
                    nn.init.constant_(m.bn2.weight, 0)  # type: ignore[arg-type]

    def _make_layer(
        self,
        block: Type[Union[BasicBlock, Bottleneck]],
        planes: int,
        blocks: int,
        stride: int = 1,
        dilate: bool = False,
    ) -> nn.Sequential:
        norm_layer = self._norm_layer
        downsample = None
        previous_dilation = self.dilation
        if dilate:
            self.dilation *= stride
            stride = 1
        if stride != 1 or self.inplanes != planes * block.expansion:
            downsample = nn.Sequential(
                conv1x1(self.inplanes, planes * block.expansion, stride),
                norm_layer(planes * block.expansion),
            )

        layers = []
        layers.append(
            block(
                self.inplanes, planes, stride, downsample, self.groups, self.base_width, previous_dilation, norm_layer
            )
        )
        self.inplanes = planes * block.expansion
        for _ in range(1, blocks):
            layers.append(
                block(
                    self.inplanes,
                    planes,
                    groups=self.groups,
                    base_width=self.base_width,
                    dilation=self.dilation,
                    norm_layer=norm_layer,
                )
            )

        return nn.Sequential(*layers)

    def _forward_impl(self, x: Tensor) -> Tensor:
        # See note [TorchScript super()]
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.relu(x)
        x = self.maxpool(x)

        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        x = self.layer4(x)

        x = self.avgpool(x)
        x = torch.flatten(x, 1)
        x = self.fc(x)

        return x

    def forward(self, x: Tensor) -> Tensor:
        return self._forward_impl(x)

temp= ResNet(BasicBlock, [2,2,2,2])

torchinfo#

from torchinfo import summary
summary(temp, input_size=(128,3,224,224))

==========================================================================================
Layer (type:depth-idx)                   Output Shape              Param #
==========================================================================================
ResNet                                   [128, 1000]               --
├─Conv2d: 1-1                            [128, 64, 112, 112]       9,408
├─BatchNorm2d: 1-2                       [128, 64, 112, 112]       128
├─ReLU: 1-3                              [128, 64, 112, 112]       --
├─MaxPool2d: 1-4                         [128, 64, 56, 56]         --
├─Sequential: 1-5                        [128, 64, 56, 56]         --
│    └─BasicBlock: 2-1                   [128, 64, 56, 56]         --
│    │    └─Conv2d: 3-1                  [128, 64, 56, 56]         36,864
│    │    └─BatchNorm2d: 3-2             [128, 64, 56, 56]         128
│    │    └─ReLU: 3-3                    [128, 64, 56, 56]         --
│    │    └─Conv2d: 3-4                  [128, 64, 56, 56]         36,864
│    │    └─BatchNorm2d: 3-5             [128, 64, 56, 56]         128
│    │    └─ReLU: 3-6                    [128, 64, 56, 56]         --
│    └─BasicBlock: 2-2                   [128, 64, 56, 56]         --
│    │    └─Conv2d: 3-7                  [128, 64, 56, 56]         36,864
│    │    └─BatchNorm2d: 3-8             [128, 64, 56, 56]         128
│    │    └─ReLU: 3-9                    [128, 64, 56, 56]         --
│    │    └─Conv2d: 3-10                 [128, 64, 56, 56]         36,864
│    │    └─BatchNorm2d: 3-11            [128, 64, 56, 56]         128
│    │    └─ReLU: 3-12                   [128, 64, 56, 56]         --
├─Sequential: 1-6                        [128, 128, 28, 28]        --
│    └─BasicBlock: 2-3                   [128, 128, 28, 28]        --
│    │    └─Conv2d: 3-13                 [128, 128, 28, 28]        73,728
│    │    └─BatchNorm2d: 3-14            [128, 128, 28, 28]        256
│    │    └─ReLU: 3-15                   [128, 128, 28, 28]        --
│    │    └─Conv2d: 3-16                 [128, 128, 28, 28]        147,456
│    │    └─BatchNorm2d: 3-17            [128, 128, 28, 28]        256
│    │    └─Sequential: 3-18             [128, 128, 28, 28]        8,448
│    │    └─ReLU: 3-19                   [128, 128, 28, 28]        --
│    └─BasicBlock: 2-4                   [128, 128, 28, 28]        --
│    │    └─Conv2d: 3-20                 [128, 128, 28, 28]        147,456
│    │    └─BatchNorm2d: 3-21            [128, 128, 28, 28]        256
│    │    └─ReLU: 3-22                   [128, 128, 28, 28]        --
│    │    └─Conv2d: 3-23                 [128, 128, 28, 28]        147,456
│    │    └─BatchNorm2d: 3-24            [128, 128, 28, 28]        256
│    │    └─ReLU: 3-25                   [128, 128, 28, 28]        --
├─Sequential: 1-7                        [128, 256, 14, 14]        --
│    └─BasicBlock: 2-5                   [128, 256, 14, 14]        --
│    │    └─Conv2d: 3-26                 [128, 256, 14, 14]        294,912
│    │    └─BatchNorm2d: 3-27            [128, 256, 14, 14]        512
│    │    └─ReLU: 3-28                   [128, 256, 14, 14]        --
│    │    └─Conv2d: 3-29                 [128, 256, 14, 14]        589,824
│    │    └─BatchNorm2d: 3-30            [128, 256, 14, 14]        512
│    │    └─Sequential: 3-31             [128, 256, 14, 14]        33,280
│    │    └─ReLU: 3-32                   [128, 256, 14, 14]        --
│    └─BasicBlock: 2-6                   [128, 256, 14, 14]        --
│    │    └─Conv2d: 3-33                 [128, 256, 14, 14]        589,824
│    │    └─BatchNorm2d: 3-34            [128, 256, 14, 14]        512
│    │    └─ReLU: 3-35                   [128, 256, 14, 14]        --
│    │    └─Conv2d: 3-36                 [128, 256, 14, 14]        589,824
│    │    └─BatchNorm2d: 3-37            [128, 256, 14, 14]        512
│    │    └─ReLU: 3-38                   [128, 256, 14, 14]        --
├─Sequential: 1-8                        [128, 512, 7, 7]          --
│    └─BasicBlock: 2-7                   [128, 512, 7, 7]          --
│    │    └─Conv2d: 3-39                 [128, 512, 7, 7]          1,179,648
│    │    └─BatchNorm2d: 3-40            [128, 512, 7, 7]          1,024
│    │    └─ReLU: 3-41                   [128, 512, 7, 7]          --
│    │    └─Conv2d: 3-42                 [128, 512, 7, 7]          2,359,296
│    │    └─BatchNorm2d: 3-43            [128, 512, 7, 7]          1,024
│    │    └─Sequential: 3-44             [128, 512, 7, 7]          132,096
│    │    └─ReLU: 3-45                   [128, 512, 7, 7]          --
│    └─BasicBlock: 2-8                   [128, 512, 7, 7]          --
│    │    └─Conv2d: 3-46                 [128, 512, 7, 7]          2,359,296
│    │    └─BatchNorm2d: 3-47            [128, 512, 7, 7]          1,024
│    │    └─ReLU: 3-48                   [128, 512, 7, 7]          --
│    │    └─Conv2d: 3-49                 [128, 512, 7, 7]          2,359,296
│    │    └─BatchNorm2d: 3-50            [128, 512, 7, 7]          1,024
│    │    └─ReLU: 3-51                   [128, 512, 7, 7]          --
├─AdaptiveAvgPool2d: 1-9                 [128, 512, 1, 1]          --
├─Linear: 1-10                           [128, 1000]               513,000
==========================================================================================
Total params: 11,689,512
Trainable params: 11,689,512
Non-trainable params: 0
Total mult-adds (Units.GIGABYTES): 232.20
==========================================================================================
Input size (MB): 77.07
Forward/backward pass size (MB): 5087.67
Params size (MB): 46.76
Estimated Total Size (MB): 5211.49
==========================================================================================

torchinfo는 요즘은 torchsummary, torchsummaryX가 update를 하지않는 상황에서 좋은 대안이다. 물론 필요 memory를 계산하는데 시간이 꽤나 걸리는 것 같지만, GPU 메모리를 고려해서 얼마나의 batch size를 미리 생각해보는데 좋은 tool로 보인다.

Netron#

# import torch.onnx
# params = temp.state_dict()
# dummy_data = torch.empty(1,3,224,224,dtype=torch.float32)
# torch.onnx.export(temp, dummy_data,'onnx_test.onnx')

================ Diagnostic Run torch.onnx.export version 2.0.0 ================
verbose: False, log level: Level.ERROR
======================= 0 NONE 0 NOTE 0 WARNING 0 ERROR ========================

../../_images/onnx_test.svg — Fig. 12 onnx로 그려보고 svg로 저장한 resnet18.#

여기서 W는 weight를 나타내고 순으로 표시된다. 그리고 B는 bias이다.

Result#

ILSVRC’15#

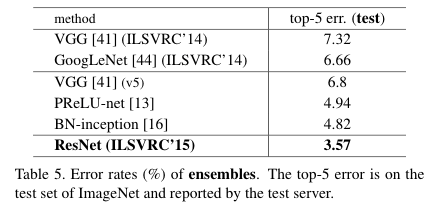
../../_images/resnet_imagenet.png — Fig. 13 “ImageNet Large Scale Visual Recognition Challenge” ILSVRC는 2010년부터 2017년까지 매년 개최된 이미지 인식 대회#

2011 XRCE
2012 AlexNet(8 cnn 3 fc)
2013 ZFNet(alexnet보다 좀더 깊게, 더 작은 필터)
2014 GoogleNet(여러 필터 병령 적용 inception module) - VGG(간단 alex 보다 deep)
2015 ResNet
2016 GoogleNet-v4
SENet(squeeze and excitation module channel간의 의존성 강조)

Reference#

source - title